底辺高さ2 証明

感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社
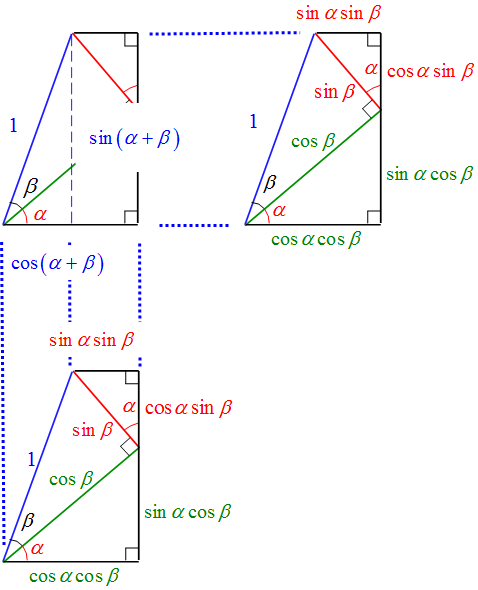
加法定理を図で示す
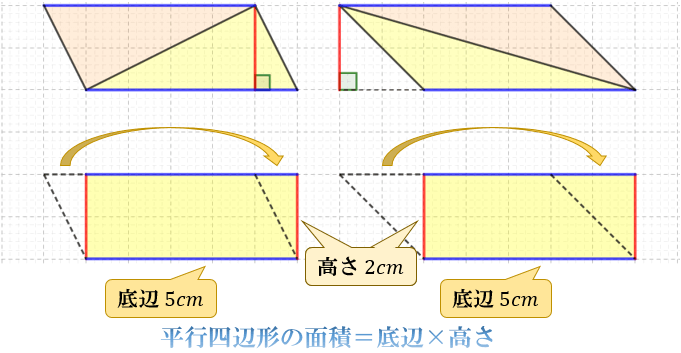
三角形の面積の求め方 なぜ底辺 高さ 2で求まるのか アタリマエ

直角三角形の辺の長さ 合同条件 面積について アタリマエ

三角形の面積を求める方法は何通り その1 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog
台形の面積の公式について 上辺と底辺の和の1 2の値に高さ値を掛けると求 Yahoo 知恵袋
ワイ「なんで2で割るんや…」 先生「ぺちゃくちゃ」 人間達「はーい!」 ワイ「三角形を2つ足したら四角形になるから四角形の面積を出して2つに割る…?あ!そういうことか!」 ─テスト後─.
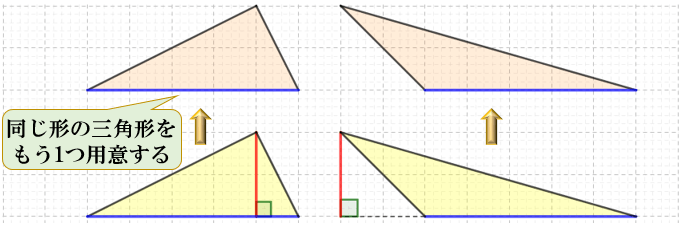
底辺高さ2 証明. 一般に三角形の面積は「底辺 × 高さ ÷ 2」により求めることができます。. ヘロンの公式 三角形の面積を求める公式にヘロンの公式というものがあります。これまで 底辺×高さ÷2 サインを使って三角形の面積を求める公式 内接円をもつ三角形の面積を求める公式 と三角形の面積を求める公式をたくさん学んできましたが、数学. 数学・算数 - 三角形の面積の公式は、「底辺×高さ÷2」です。 「なんで2で割るの?」と聞かれたら、答えは簡単。 「この三角形と同じ三角形を上下ひっくり返してくっつけてごらん。 平行四辺形になったでし.
底辺×高さ÷2(三角形の面積)の公式を適用すればいい。 底辺(\(t\) )と高さ(\(gt\) )の積に\(\frac{ 1 }{ 2 }\) をかけた値が三角形の面積だ。 これを下側の面積と合わせれば、以下の式となり全体の面積を表すことになる。. 先生「四角形は三角形2つなので四角形の面積を求めて2で割ればいいから、底辺×高さ÷2で導けます」 人間達「はーい!」 イッチ「なんでや…」 先生「では次の問題へ進みます」 人間達「はーい!」 ワイ「なんで2で割るんや…」 先生「ぺちゃくちゃ」. 三角形の面積はなぜ底辺×高さ÷2で求められるの? 三角形は大きく分けて3種類あります。 直角三角形 1) 3角形の角のうち1つが90°である三角形のことをいいます。 、鋭角三角形 2) 三角形の3つの角、全てが90°より小さい三角形のことをいいます。 、鈍角三角形 3) 三角形の角のうち1つの角が90.
底辺×高さ÷2ってのは 三角形の面積の式ですから直角三角形にこだわる必要はありませんよ 対角線を一本引いてみてください すると底辺をa、高さhの三角形と、底辺をb、高さhの三角形の二つに切ることができるでしょ 底辺aの三角形の面積はah/2 底辺bの三角形の面積はbh/2 二つの和がこの台形だからah/2+bh/2=(a+b)h/2 他にもこの台形をひっくり返したものを横にひっ付けたら辺が(a+b)で高さhの平行四辺形となるので 平行四辺形の面積は辺の長さ×高さだから(a+b)h この平行四辺形は元の台形を二つ繋いだものなので台形の面積はこの半分で(a+b)h/2ってのもありますが 台形の公式悩んでる状態なら対角線で三角形二つに区切って二つの三角形の面積足す方がわかりやすいかも. 底辺の長さ×高さ÷2 ですよ。 証明は中学校の幾何で学ぶとして・・・ 底辺×高さ===すなわち長方形の面積ですから・・ 長方形を高さを変えずに変形させて、 面積 = 底辺の長さ×高さ. まとめ (1) 図9ののように2つの三角形の底辺の比が a:b ,高さの比が m:n のとき,面積の比は am:bn になる.(右の図9では高さの比を m:n と読む.)-- 図9 --(2) 図10のような図形において,3つ以上の三角形の面積を比較するときは,次のように「比の値」を「分数」にすると簡単にできる..
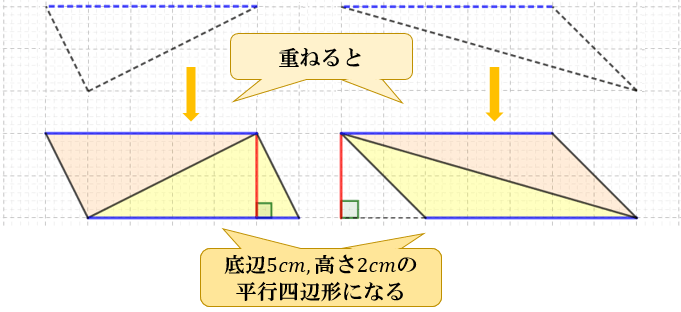
底辺×高さ÷2 というのは、底辺と高さでできる、長方形の面積の半分ということです。 左側の三角形は、高さの点線で分けて、「1」と「2」の三角形は、それぞれ、同じ高さの長方形の面積の半分です。だから、面積は、底辺×高さ÷2 で求められます。. 先ほど確認したとおり、三角形の面積は「(底辺)×(高さ)×$\frac{1}{2}$」です。 底辺の比は、相似比なので、1:2。 高さの比も相似比と同様に1:2ですね。 どちらの三角形の面積も$\frac{1}{2}$をかけるので、 ABC: A’B’C’=1×1:2×2=1=4となります。 この. まとめ (1) 右図9ののように2つの三角形の底辺の比が a:b ,高さの比が m:n のとき,面積の比は am:bn になる.(右の図9では高さの比を m:n と読む.) (2) 右図10のような図形において,3つ以上の三角形の面積を比較するときは,次のように「比の値」を「分数」にすると簡単にできる..
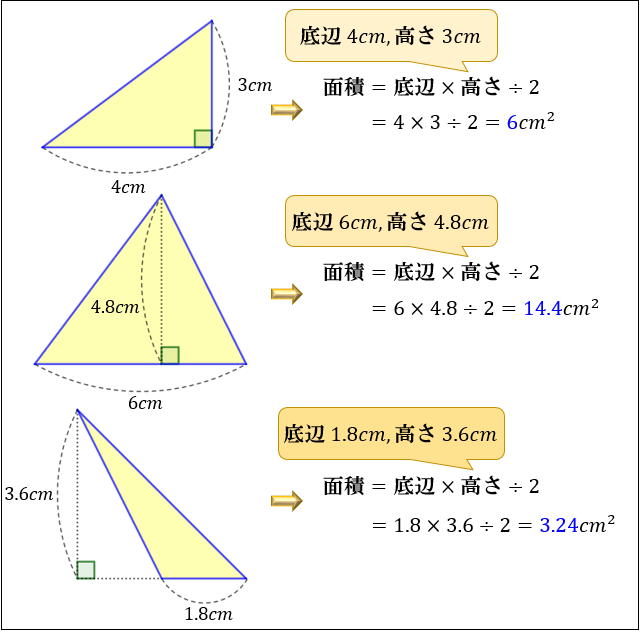
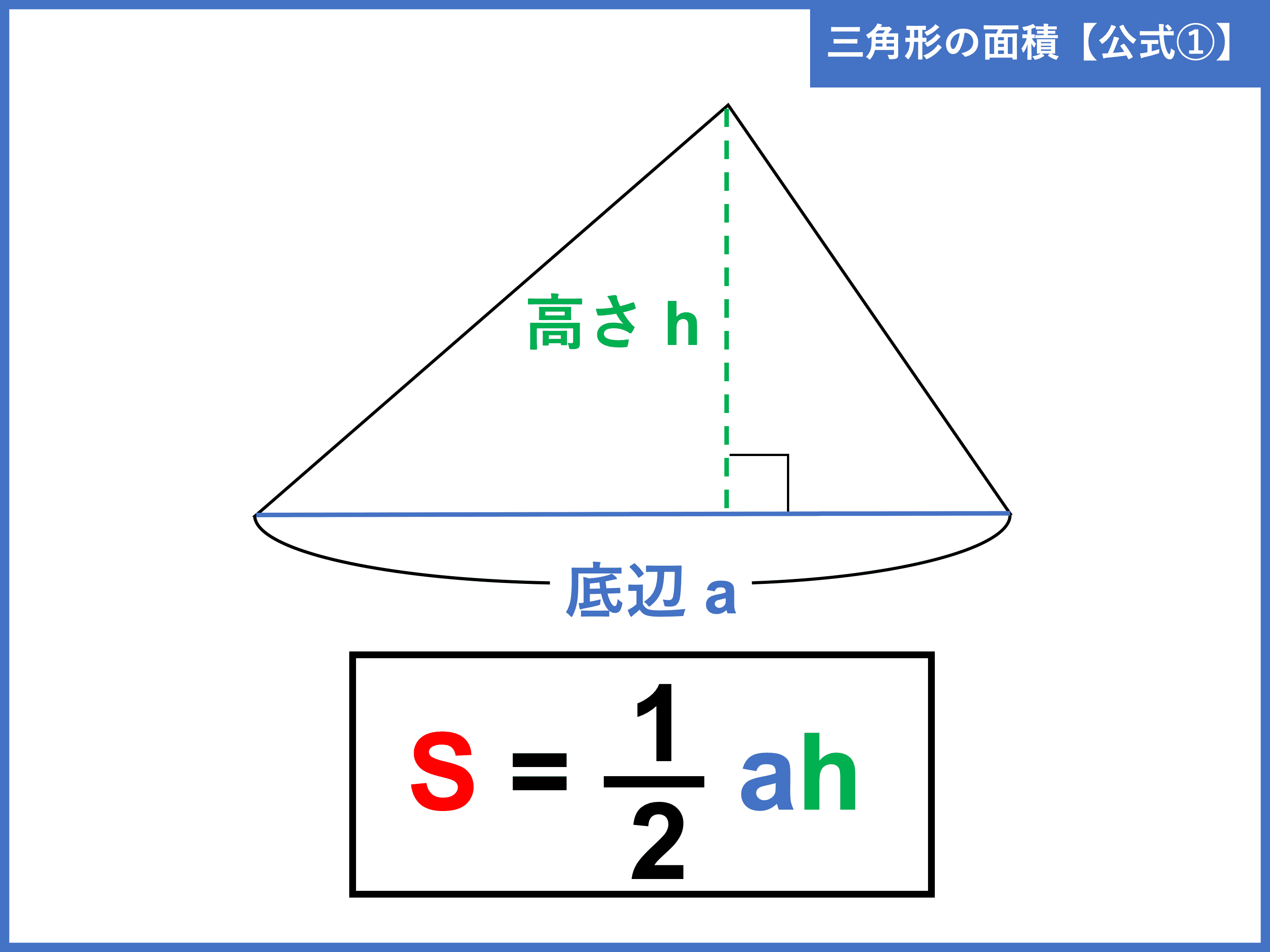
角柱の体積が角錐(すい)の体積の 3分の1 になる理由を書いておきます。 ここで、 次の2点は既知とします。 底面積と高さが同じ角錐は同じ体積になる。 (これもいつか証明を書きます。) 角柱の体積は底面積と高さの積である。 説明 ここでは三角錐について考えます。. 上図のようにどんな形をした三角形であっても、その面積は 公式 「三角形の面積 底辺 高さ 」 「 三 角 形 の 面 積 = 底 辺 × 高 さ ÷ 2 」 で求まります。. 三角形の面積は「 \(底辺×高さ÷2\) 」という公式から求まりますが、この公式以外にも色々な方法で三角形の面積を求めることができま … 数学の疑問.
変数の型 任意の変数名 = メソッド名(底辺,高さ)である。 ※calcTriangleArea(10.0, 5.0)で、定義の呼び出し、引数( )に値10.0と5.0を渡し、double triangleAreaへ代入という事を、まとめて行っている。 ※÷2は、calcTriangleAreaメソッドで定義されてるので、記述はいらない。. (2)の正答例 平行四辺形の面積=底辺×高さ (3)の正答例 底面積 説明 三角柱の体積は,角柱の体積の公式を使って求 めることができる。 底面の形が直角三角形なので,三角形の面積の 公式を使って底面積を求めると, 4×3÷2と表すことができる。. 三角形の面積は「 底辺 高さ 底 辺 × 高 さ ÷ 2 」という公式から求まりますが、この公式以外にも色々な方法で三角形の面積を求めることができます。.
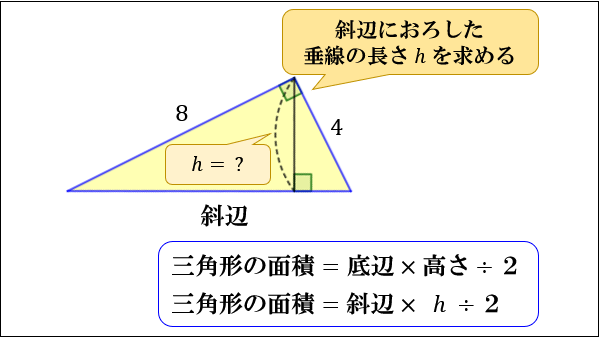
ヘロンの公式を証明します。まず三角形ABCを考えます。 角 \( A, B, C \) に向かい合う辺をそれぞれ \( a, b, c \) とします。ABCbcaここで三角形の面積が \( \frac{1}{2} bc \sin A \) で表されることは既知とします。 ヘロンの公式 三角形の面積 \( S \) は. ところで三角形の面積を求めるには、底辺×高さ÷2をすればよかった。この ABCの面積Sは で求めることができる。 さきほど であると求めたので、これを三角形の面積の公式に代入をする。すると が求まる。. 三角形の面積を求める公式 三角形の面積を求める公式といえば「底辺×高さ÷2」を思い出しますが、ここでは「サインを使って三角形の面積を求める公式」を紹介します。 図のような abcの面積をsとしたとき 公式の証明 ではこの公式を証明してい.
中2数学:等積変形と面積比についての復習 新中3生のみなさん / 中2英語を復習したいみなさん! ・等積変形 三角形の面積=底辺×高さ÷2 「どんな三角形も、底辺の長さと高さがそれぞれ等しければ面積は等しくなる」 これを利用するのが「等積変形」です。. 三角形の面積が (底辺)×(高さ)÷2 になる理由を説明してみます。 前提とする知識 長方形の面積は 縦×横 和と積の分配法則 直角三角形の面積を求める まずは直角三角形の面積を考えます。 直角三角形は長方形を2分割したものなので、直角をはさむ2辺の積を2で割ったものになります。. 先生「三角形を2つ足したら四角形になるから四角形の面積を出して2つに割るんですよ」 人間達「はーい!」 ワイ「ぺちゃくちゃ」 先生「三角形の面積は底辺×高さ÷2で導けます」 人間達「はーい!」 ワイ「なんでや…」 先生「では次の問題へ進みます」.
三角形の面積 上記のような三角形ABCの面積Sを求めよという問題があるとします。 本来であれば三角形の面積は「面積=底辺×高さ÷2」で求めることができますが、上記のように高さが与えられていない三角形が出題されるときがあります。 こ. 扇形の半径を三角形の底辺と見れば 、 弧の長さは三角形の高さと同一視できます 。 すると先ほどの 扇形の面積の公式は三角形の面積の公式、(底辺)×(高さ)÷2、そのものです 。.
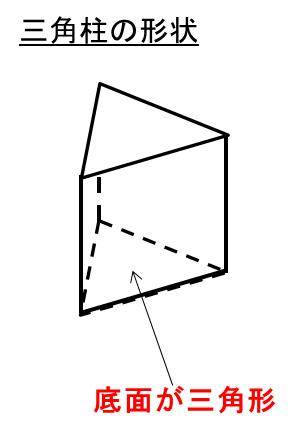
三角柱の表面積 底面積も と体積を求める公式と計算問題 単位との関係 ウルトラフリーダム

三角形の面積の公式 2 って どうして2で割るの

Mathematics 等積変形 面積と平行線 働きアリ

面積比 中学数学に関する質問 勉強質問サイト

面積の求め方 計算公式一覧
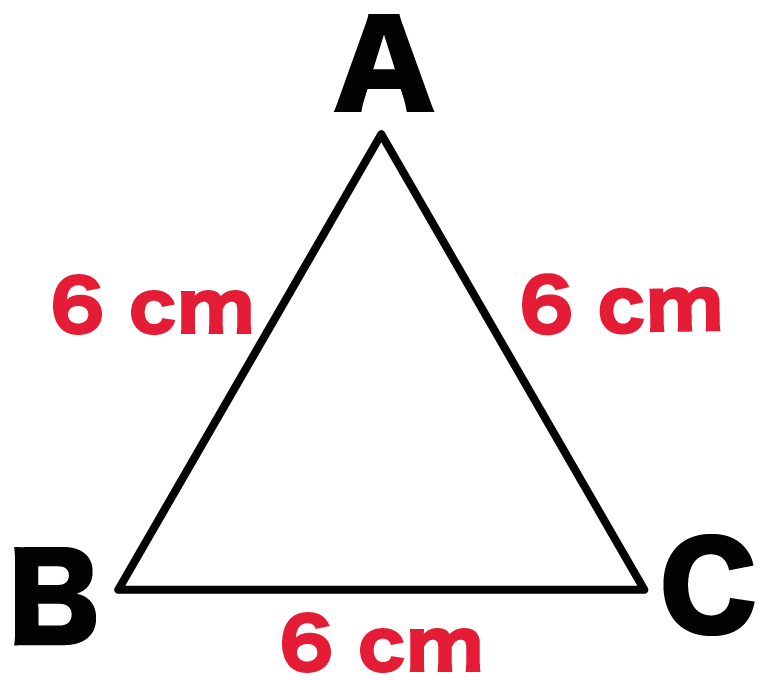
簡単公式 正三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
小学生の算数の問題です どなたか助けてください 平行四辺形abc Yahoo 知恵袋

三角形の角の二等分線と線分の比 個別指導学院core コア 西川口の個別指導塾

高校数学 三角比による三角形の面積の公式 S 1 2bcsina の証明と利用 受験の月

中2数学証明ですぜひご回答をお願いします 中学数学に関する質問 勉強質問サイト
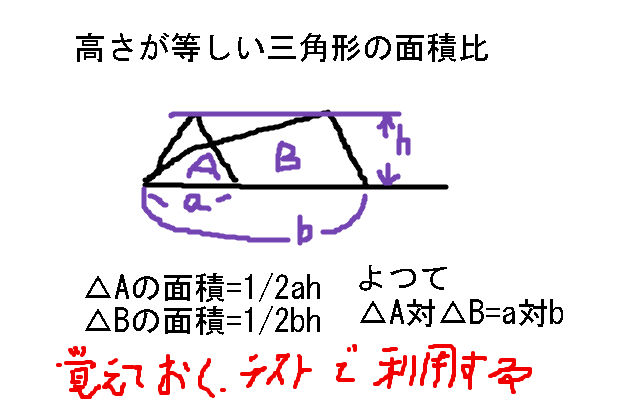
高さが等しい三角形の面積比の証明 中学数学 寺子屋塾の復習サイト
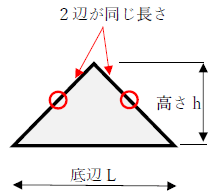
二等辺三角形の面積は 1分でわかる計算 公式 角度 高さがわからない場合の計算

3 の答えは26なのですが どこが底辺で高さなのかもよくわかりません どのように Clear

三角形の面積の公式 2 って どうして2で割るの
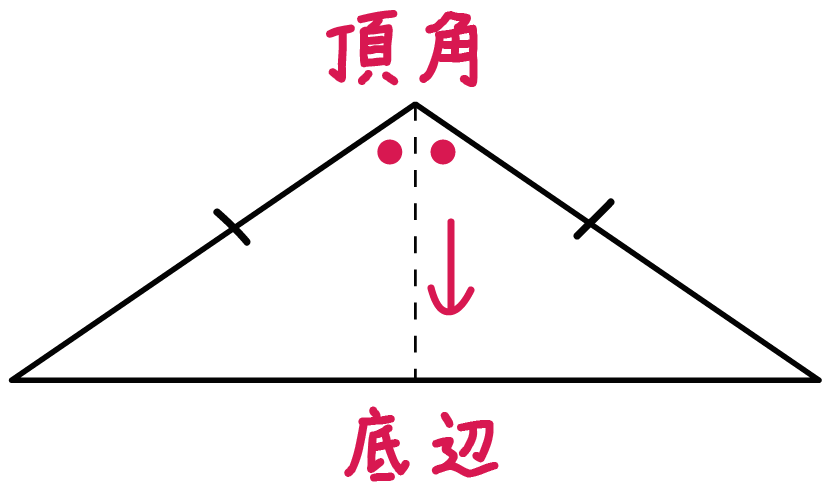
簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

三平方の定理とヘロン三角形の話

数学 中二 二等辺三角形の性質 中学数学に関する質問 勉強質問サイト

教材総合カタログ 19 小学校全教科

三角形の頂角の2等分線が底辺をわけるときの比 身勝手な主張
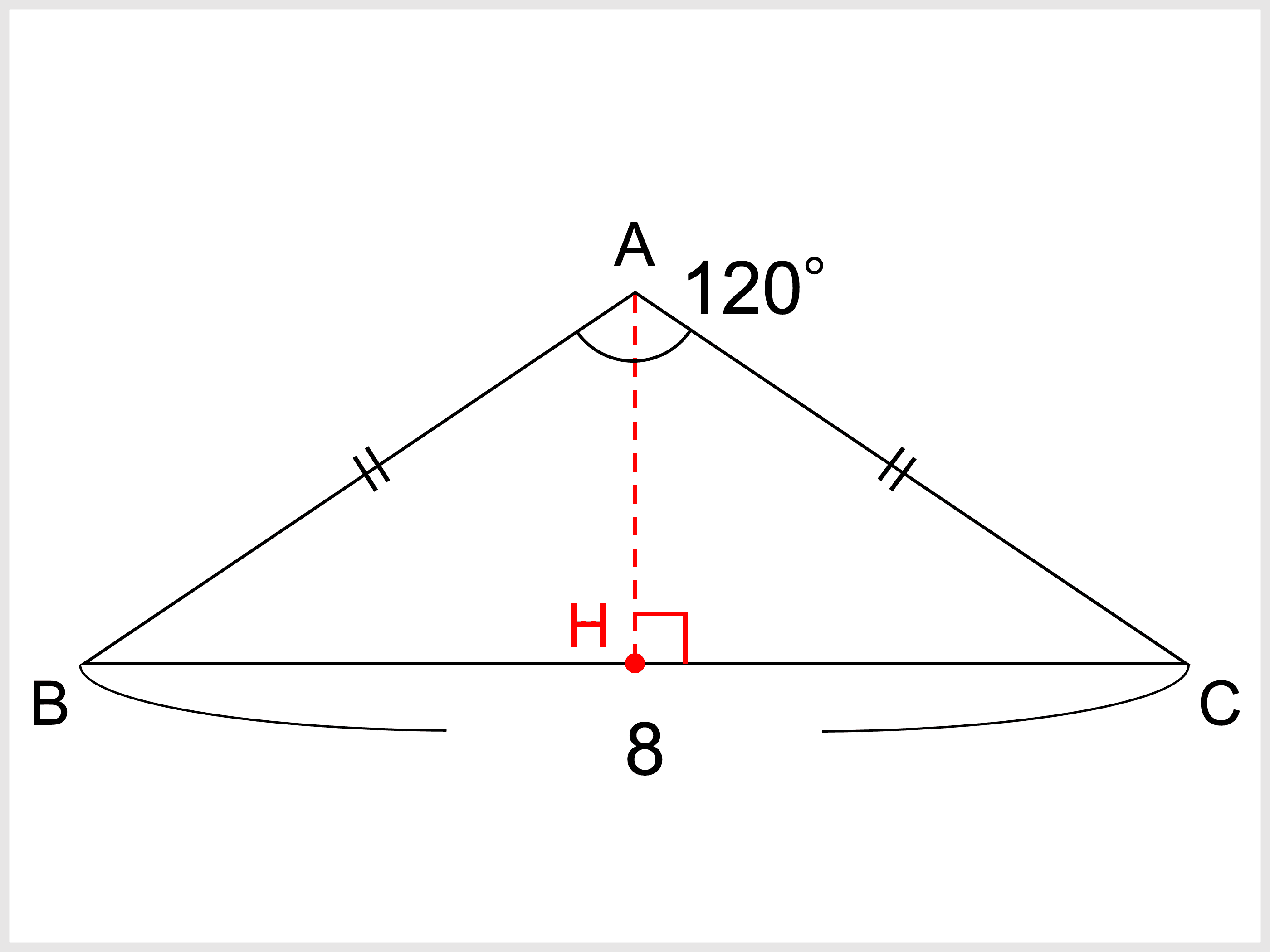
二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典
なぜ三角形は底辺 高さ 2なのですか どうして 2がはいるのです Yahoo 知恵袋

平行四辺形の面積の求め方 公式と計算例
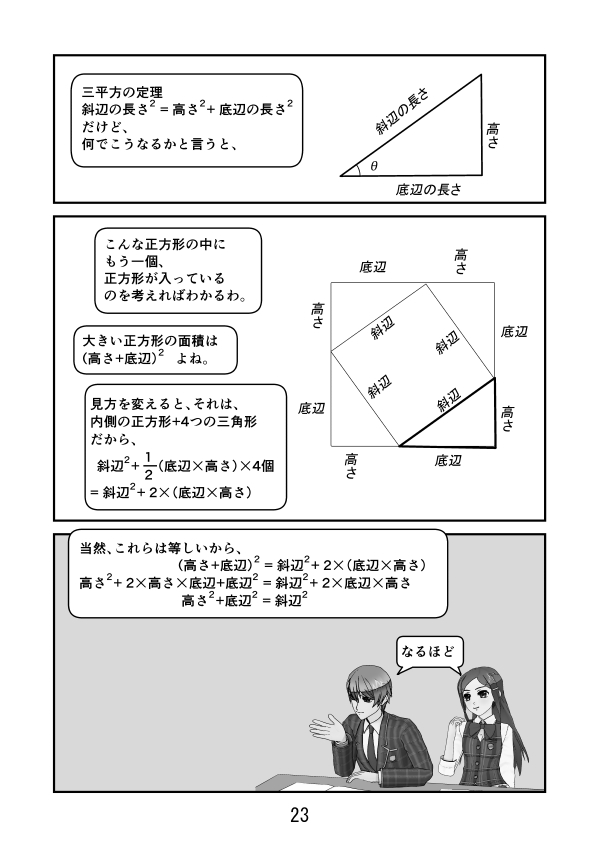
漫画で高校数学 三角形で Tan8 Sin8 Cos8と Sin8 2 Cos8 2 1の証明 三角関数8 Manabi100
直角三角形の辺の長さ 合同条件 面積について アタリマエ
ベクトルによる三角形の面積の求め方 公式や証明 計算問題を徹底解説 受験辞典
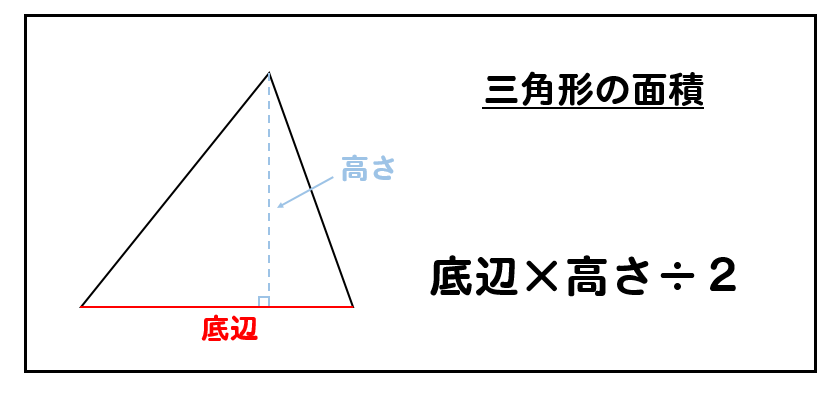
三角形の面積公式 小学生はどうやって解く 問題を使って解説 数スタ

面積が12cm の三角形の底辺xcmと高さycm この下の図と上の問題で質問で 中学校 教えて Goo

高校数学 三角比を利用した長さの求め方2 映像授業のtry It トライイット
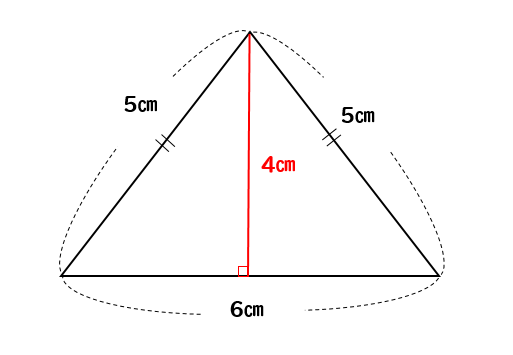
高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ

三角形の合同ではなく直角三角形の合同条件で求めることはできま 中学数学に関する質問 勉強質問サイト

2 は理解してるけど 1 がわかりませんなぜかな証明の仕方 高校数学に関する質問 勉強質問サイト
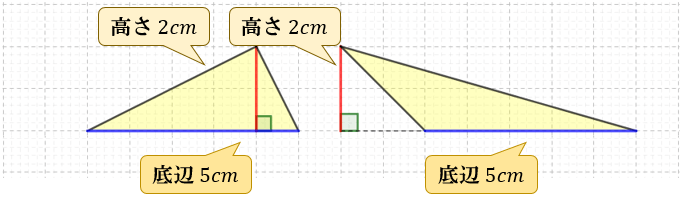
三角形の面積の求め方 なぜ底辺 高さ 2で求まるのか アタリマエ

この問題の証明を2枚目のように解いたのですが丸になりますかね ちなみに解答は3枚目で Clear

3分で分かる 平行四辺形とは 定義や性質 成立条件をわかりやすく 合格サプリ
2

三角形の面積を求める公式7選 高校数学のまとめにどうぞ
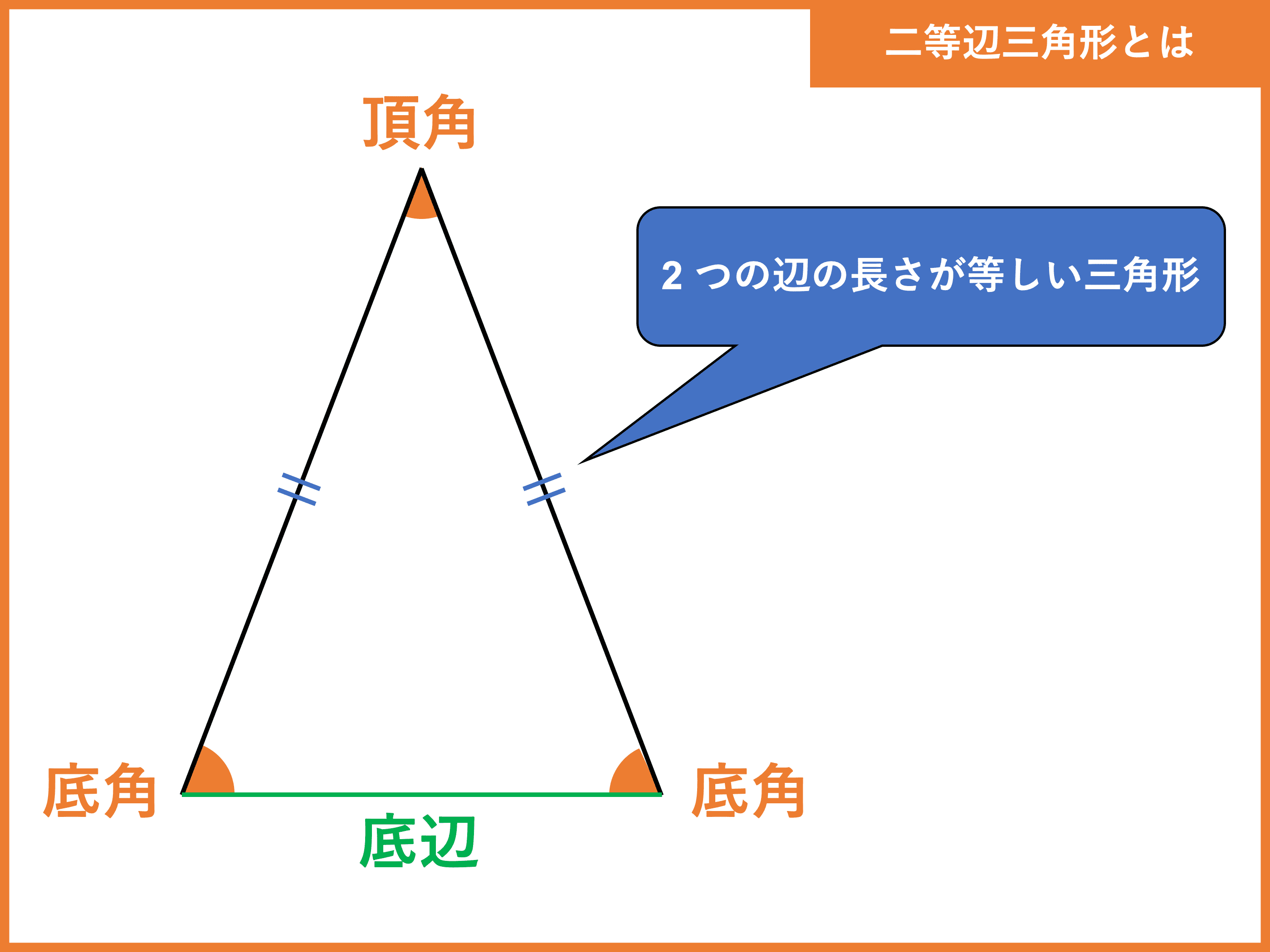
二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典

Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集

三角形の面積の求め方とは Sinやベクトルを用いる公式も解説 小学生から高校生まで 遊ぶ数学
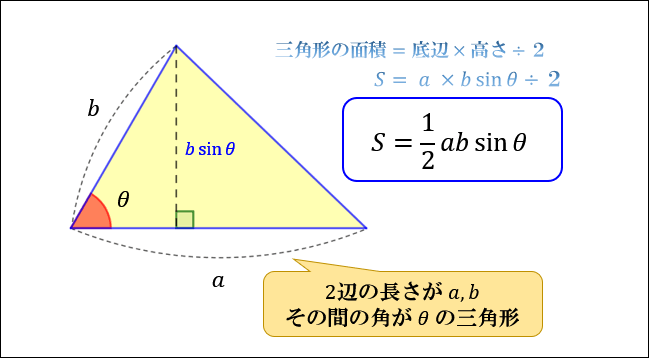
三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
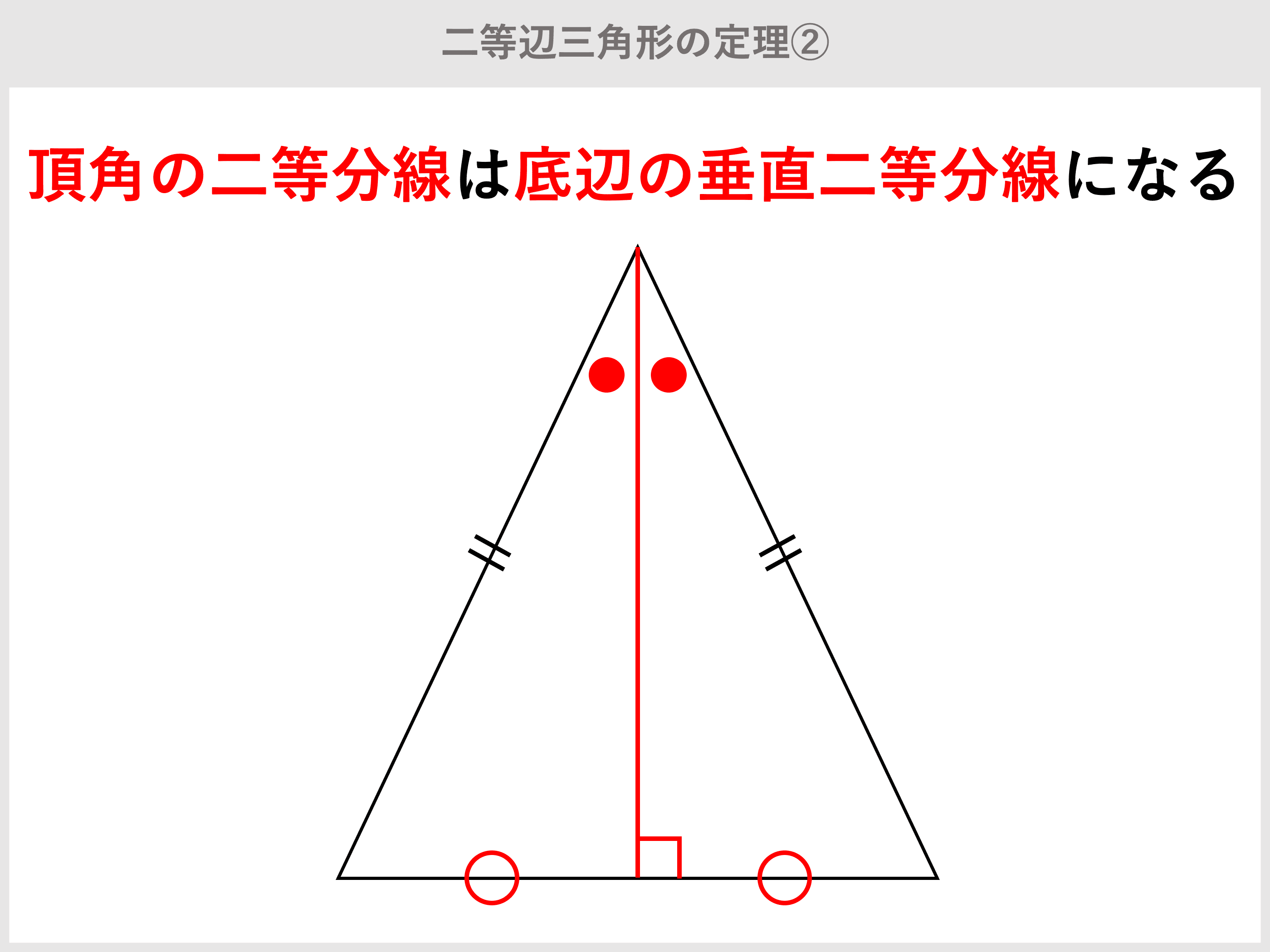
二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典

数学 4 と 5 の問題 中学数学に関する質問 勉強質問サイト

三角形の面積の求め方とは Sinやベクトルを用いる公式も解説 小学生から高校生まで 遊ぶ数学
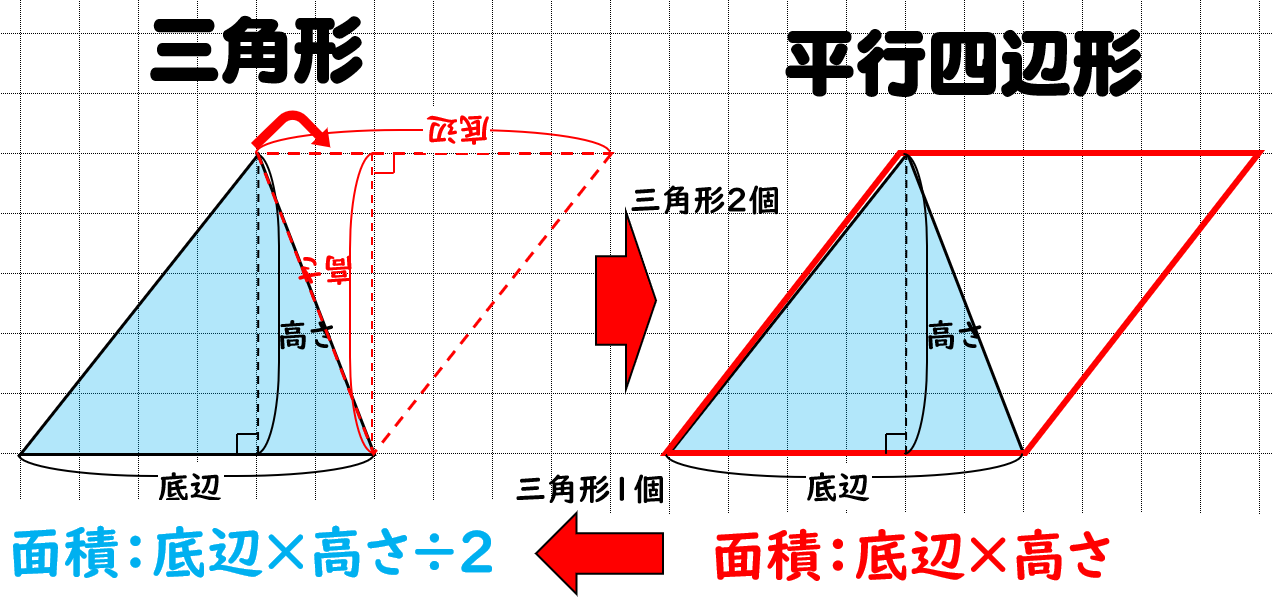
三角形の面積の公式 小学生に教えるための分かりやすい解説 数学fun
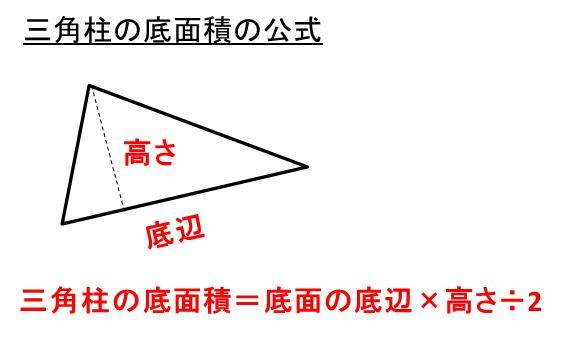
三角柱の表面積 底面積も と体積を求める公式と計算問題 単位との関係 ウルトラフリーダム

三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ

平行線と面積のポイント 数学教材

直角三角形の辺の長さ 合同条件 面積について アタリマエ

1の式がy 2分の1かけるxかける6になる 理由を教えてください Clear
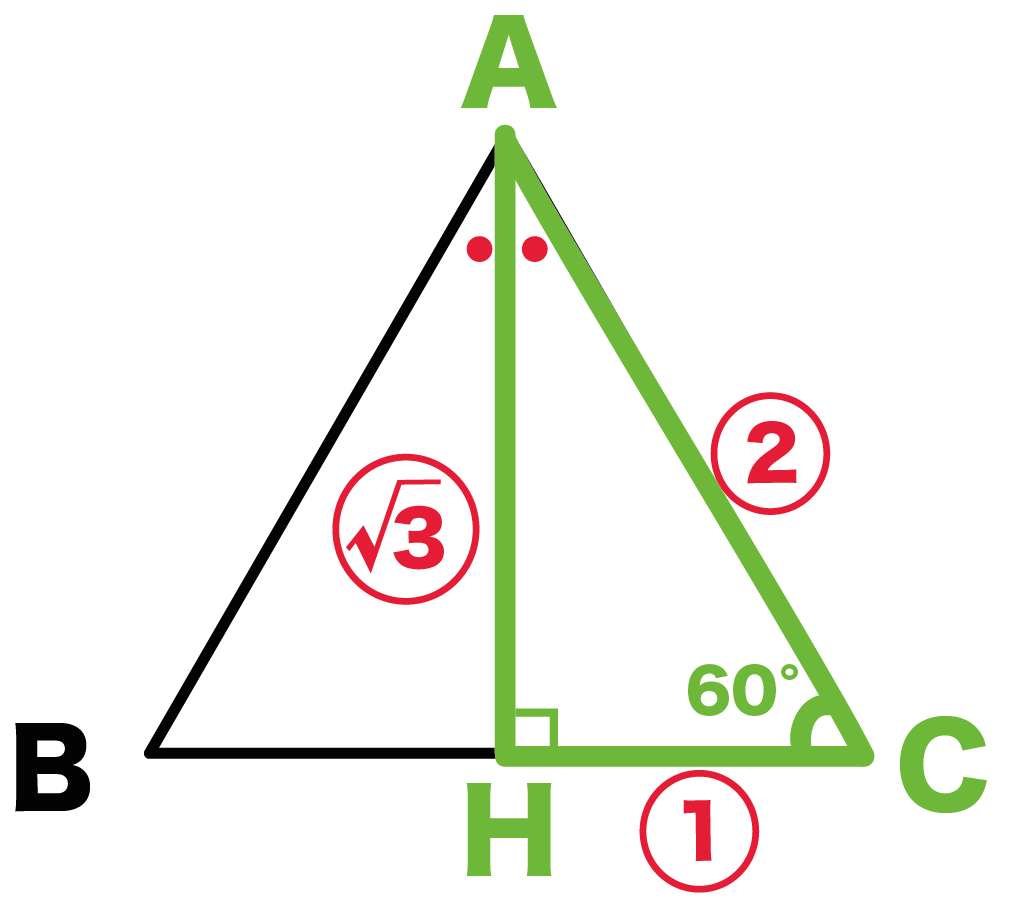
簡単公式 正三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

この問題について教えてください 高校数学に関する質問 勉強質問サイト
正方形と正三角形が組み合わさった図形の面積計算 定義公式が小学範囲なら何でもアリな中学受験
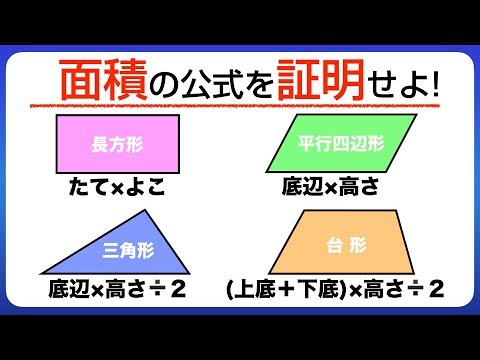
算数クイズ 公式の証明 面積 まだ習っていない小学生にわかるように説明してください 解説あり 中学入試 Youtube
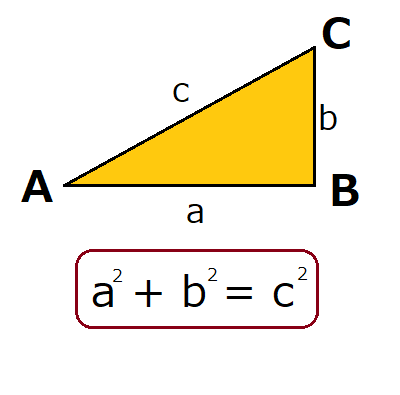
三平方の定理の証明 中学生向けの方法を6つ紹介 ヒデオの情報管理部屋
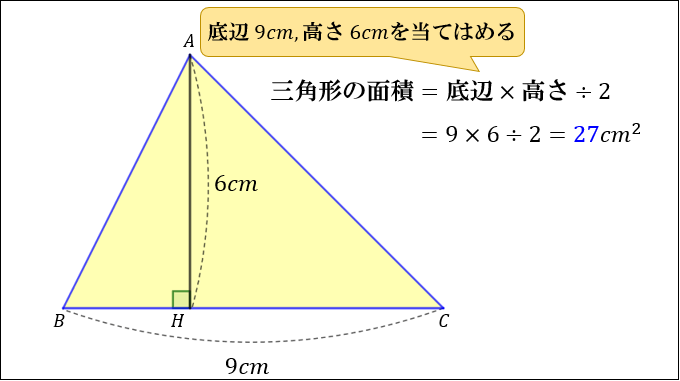
三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ

三角形の面積比 数学の偏差値を上げて合格を目指す
三角形の面積の求め方 なぜ底辺 高さ 2で求まるのか アタリマエ
三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典

教えてください 中三の数学です Clear

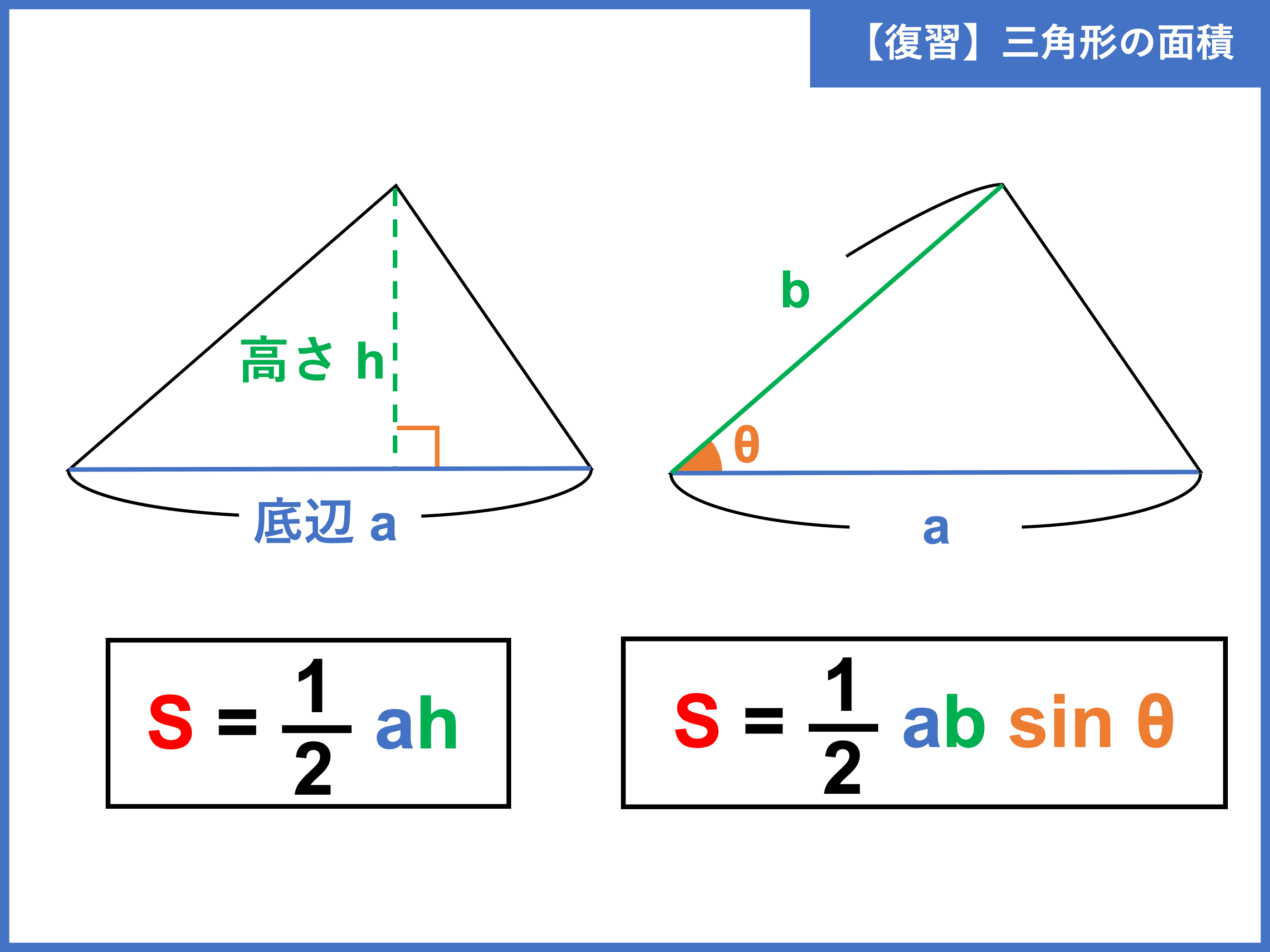
サイン Sin を使った三角形の面積を求める公式とその証明 数学i By ふぇるまー マナペディア
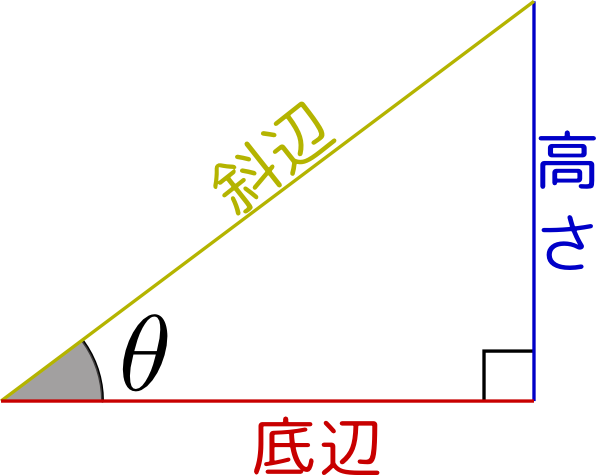
三角形の辺の比による三角関数の定義

赤線の高さを含んだ直角三角形の2つは 高校数学に関する質問 勉強質問サイト
Static Tokyo Np Co Jp Pdf Article B964cdbc3adcd1e2 Pdf
三角形の面積の求め方 なぜ底辺 高さ 2で求まるのか アタリマエ

三角形の面積はなぜ底辺 高さ 2なの 鋭角三角形 直角三角形 鈍角三角形のそれぞれについて解説します みけねこ小学校

相似 台形と面積比の問題を徹底解説 数スタ

中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ
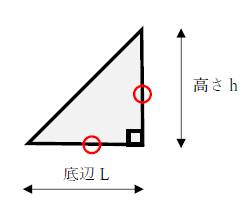
二等辺三角形の底辺は 1分でわかる意味 長さの計算 角度 高さ 三平方の定理との関係
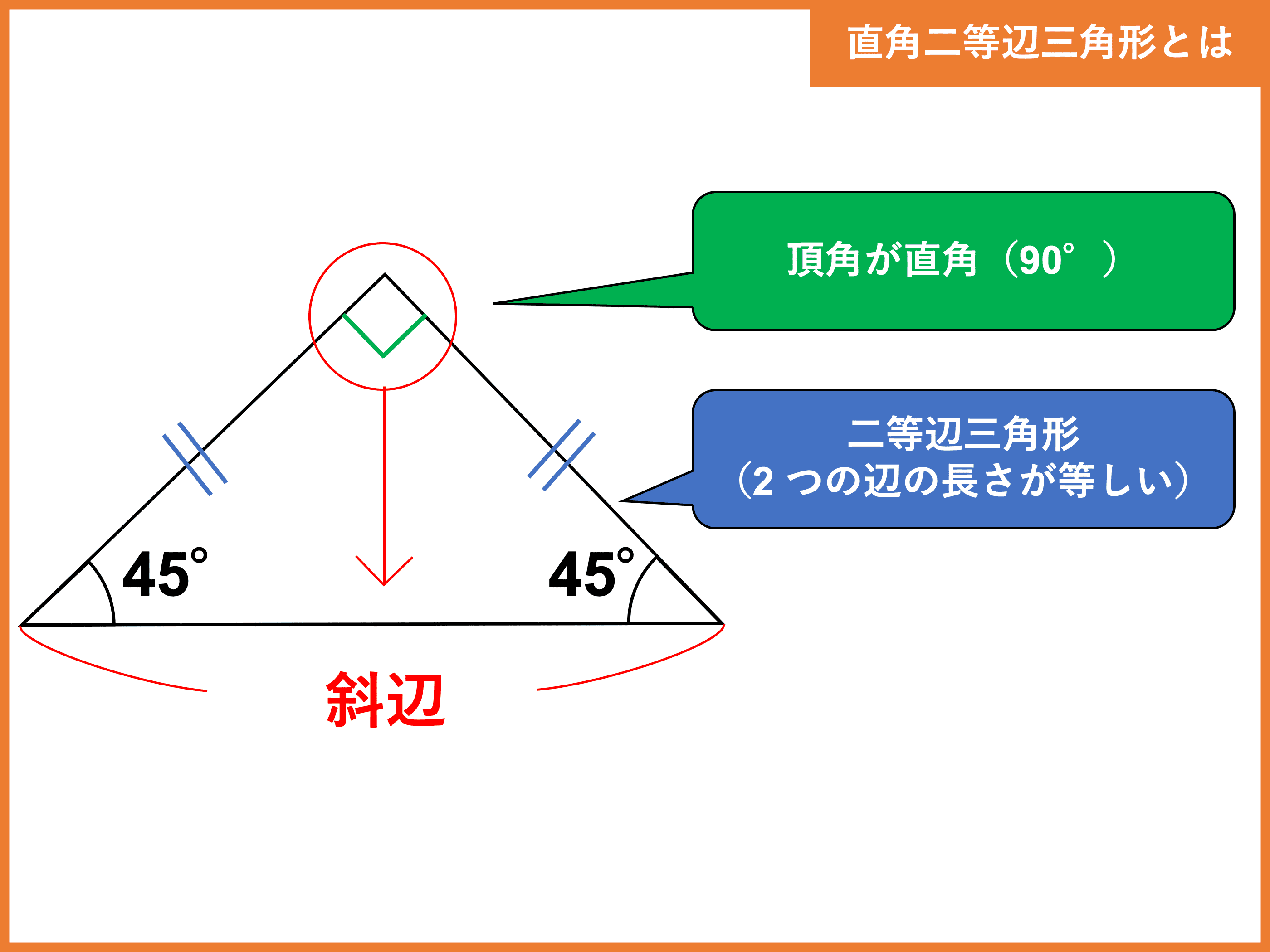
直角二等辺三角形とは 定義 公式 定理や 辺の長さの比 証明問題などをわかりやすく解説 受験辞典

簡単公式 直角二等辺三角形の面積の2つの求め方 Qikeru 学びを楽しくわかりやすく
例題1 正方形を固定し 直角二等辺三角形を秒速2cmで 点cと点eが重な Yahoo 知恵袋

三角形の面積の求め方とは Sinやベクトルを用いる公式も解説 小学生から高校生まで 遊ぶ数学

三角形の面積の求め方は 底辺 高さ 2ですよね でもある動画で 三 中学校 教えて Goo

高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト
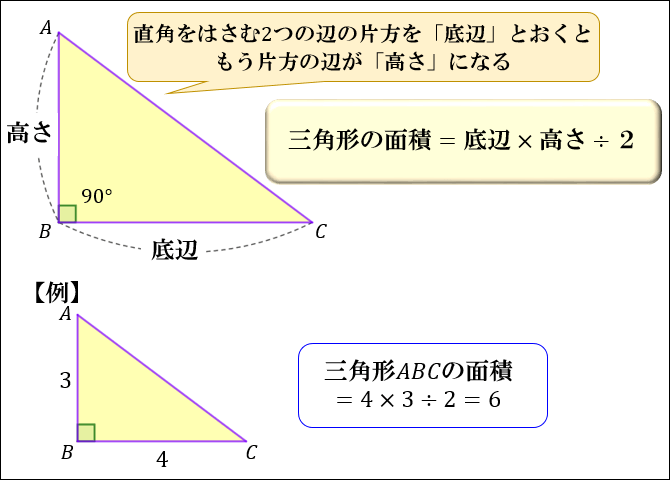
直角三角形の辺の長さ 合同条件 面積について アタリマエ
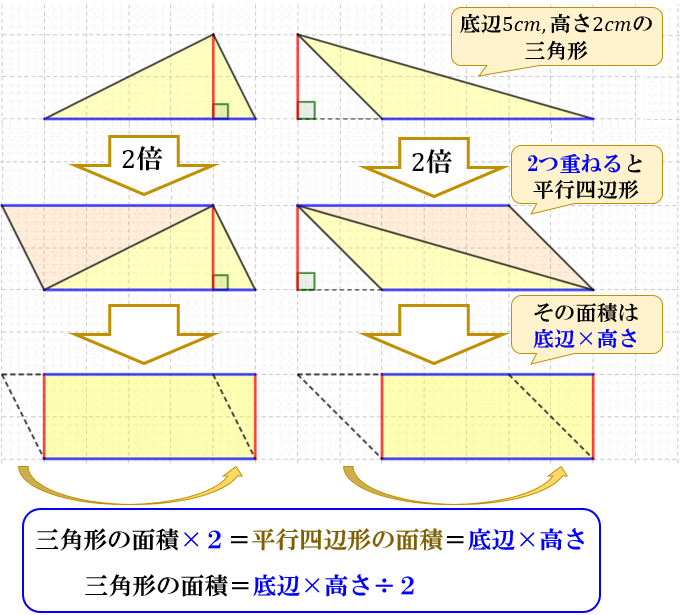
三角形の面積の求め方 なぜ底辺 高さ 2で求まるのか アタリマエ
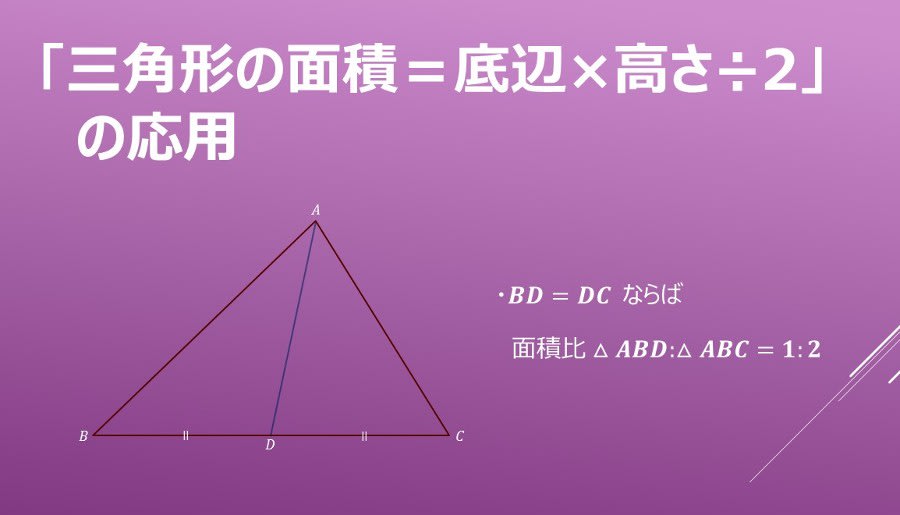
高校入試と 等積変形や図形の面積比について 中学生 受験対応 英語 数学 学習講座

高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト

二等辺三角形に関するある問題 底辺 高さそして面積 身勝手な主張

三角形の面積の求め方とは Sinやベクトルを用いる公式も解説 小学生から高校生まで 遊ぶ数学
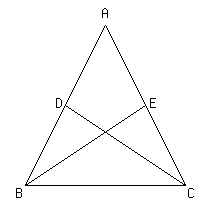
二 等辺 三角形 定理 二等辺三角形と定理 定義

三角形の面積の公式 2 って どうして2で割るの

数学 数学教育 のブログ記事一覧 222ページ目 身勝手な主張
三角形の面積は 底辺 高さ 2 で求めることができます なぜ Yahoo 知恵袋

中学校数学 証明のコツ 入試で差がつく 面積の比 体積の比 を得意にできる教材

高校数学 体積の計算 2 問題編 映像授業のtry It トライイット

外積の長さ 平行四辺形の面積 証明 理数アラカルト

簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
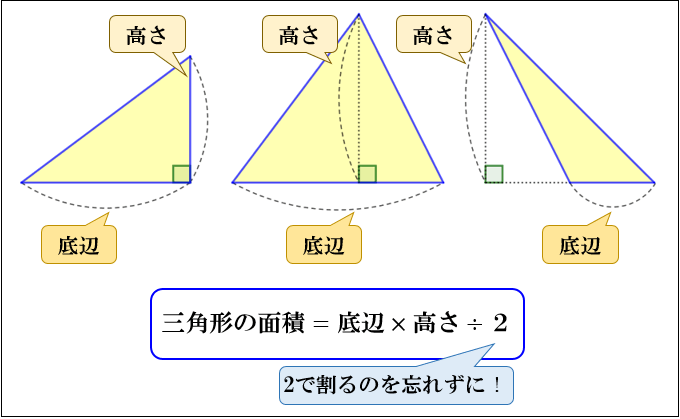
三角形の面積の求め方 なぜ底辺 高さ 2で求まるのか アタリマエ
5d91uwmjd96pmm

3 36なのですが 底辺の出し方がわかりません 高さの4センチはわかりました Clear
三角形の面積の求め方 なぜ底辺 高さ 2で求まるのか アタリマエ

公式の証明 体積測定によって検証する土塁の取崩しと土橋の造成
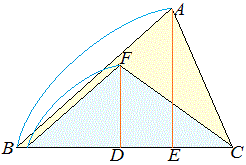
面積比



